Logarithms are used to find the number to which the base must be raised in order to become the value in the logarithm.
This is the method used when solving a logarithm problem:
If logax = N, then aN = x.
I will work through two examples:
Example #1:
log1010,000 = x
10x = 10,000
x = 4
Example #2:
log612x = 2
62 = 12x
36 = 12x
x = 3
Natural logarithms, represented by ln, are logarithms with the base of e.
This is the method used when solving a natural logarithm problem:
If ey = x, then ln(x) = y.
I will work through an example:
ex = 30
ln(ex) = ln(30)
x = ln(30)
x = ~3.4012
Thursday, May 15, 2014
Review – Mathematical Induction
Mathematical induction is a method of proving certain formulas. It requires proving the formula for the values of n and n + 1. Here is an example:
Use mathematical induction to prove the formula for every positive integer n.
2 + 4 + 6 + 8 + . . . + 2n = n(n + 1)
First, we must prove this formula true for n = 1:
2(1) = (1)((1) + 1)
2 = 1(2)
2 = 2
Next, we must assume that the formula is true for n, and attempt to prove it for n + 1:
2 + 4 + 6 + 8 + . . . + 2(n + 1) = (n + 1)((n + 1) + 1)
2 + 4 + 6 + 8 + . . . + 2n + 2 = (n + 1)(n + 2)
We can substitute the 2 + 4 + 6 + 8 + . . . with n(n + 1), since we assume that the formula is true for n:
2n + 2n + 2 = (n + 1)(n + 2)
n(n + 1) + 2n + 2 = (n + 1)(n + 2)
n2 + n + 2n + 2 = n2 + n + 2n + 2
n2 + 3n + 2 = n2 + 3n + 2
Since the left-hand side now is equal to the right-hand side, we have proven this formula true for every positive integer n.
Mathematical induction can also be used in formulas using summation (sigma) notation.
Use mathematical induction to prove the formula for every positive integer n.
2 + 4 + 6 + 8 + . . . + 2n = n(n + 1)
First, we must prove this formula true for n = 1:
2(1) = (1)((1) + 1)
2 = 1(2)
2 = 2
Next, we must assume that the formula is true for n, and attempt to prove it for n + 1:
2 + 4 + 6 + 8 + . . . + 2(n + 1) = (n + 1)((n + 1) + 1)
2 + 4 + 6 + 8 + . . . + 2n + 2 = (n + 1)(n + 2)
We can substitute the 2 + 4 + 6 + 8 + . . . with n(n + 1), since we assume that the formula is true for n:
2n + 2n + 2 = (n + 1)(n + 2)
n(n + 1) + 2n + 2 = (n + 1)(n + 2)
n2 + n + 2n + 2 = n2 + n + 2n + 2
n2 + 3n + 2 = n2 + 3n + 2
Since the left-hand side now is equal to the right-hand side, we have proven this formula true for every positive integer n.
Mathematical induction can also be used in formulas using summation (sigma) notation.
Review – Parametric Equations
Parametric equations are a method of graphing using an additional parameter, which represents progressive variables such as time. Mostly, this variable is denoted by t. I will provide a quick example to clarify this method of graphing:
x = 2t
y = t2
First, we need to eliminate the variable t. To do this, we need to find a way to make x and y equal to the same value.
x/2 = t
√y = t
Now that t is equal to both x/2 and √y, we can simply set the following:
√y = x/2
y = (1/2)x2
Now, all we have to do is graph this equation:
Since t is not shown on the graph, we must label each point plotted on the line with t = (value of t at that point), so as to indicate the direction in which the graph is progressing. Also, an arrow can be used to indicate this direction.
First, we need to eliminate the variable t. To do this, we need to find a way to make x and y equal to the same value.
x/2 = t
√y = t
Now that t is equal to both x/2 and √y, we can simply set the following:
√y = x/2
y = (1/2)x2
Now, all we have to do is graph this equation:
We could have also graphed this by creating a table by incrementing t and then determining the values of x and y for those values of t.
Since t is not shown on the graph, we must label each point plotted on the line with t = (value of t at that point), so as to indicate the direction in which the graph is progressing. Also, an arrow can be used to indicate this direction.
Thursday, May 8, 2014
Review – Gaussian and Gauss-Jordan Elimination
Gaussian Elimination involves reducing a matrix to row-echelon form using the elementary row operations of matrices.
Gauss-Jordan Elimination involves reducing a matrix to reduced row-echelon form using the elementary row operations of matrices.
Either of these methods can be used to solve a system of equations.
Here is an example of solving the following system of equations using the Gauss-Jordan Elimination method:
Gauss-Jordan Elimination involves reducing a matrix to reduced row-echelon form using the elementary row operations of matrices.
Either of these methods can be used to solve a system of equations.
Here is an example of solving the following system of equations using the Gauss-Jordan Elimination method:
| 2x | – | y | + | 3z | = | 24 |
| 2y | – | z | = | 14 | ||
| 7x | – | 5y | = | 6 |
Review – Vectors and Dot Products
A vector is a quantity having direction and magnitude.
For any vector u = <a, b>, the magnitude is given by:
||u|| = √(a2 + b2)
For any two vectors u = <a, b> and v = <c, d>, the dot product is given by:
u • v = ac + bd
The angle between any two vectors u and v is given by:
cosθ = (u • v) / (||u|| ||v||)
Now, let us try an example of each. For these examples let
u = <6, 4>
and
v = <2, 8>.
First, let us find the magnitude of each vector:
||u|| = √(62 + 42) = √(36 + 16) = √52 ≈ 7.2
||v|| = √(22 + 82) = √(4 + 64) = √68 ≈ 8.2
Next, let us find the dot product of these vectors:
u • v = (6)(2) + (4)(8) = 12 + 32 = 44
Finally, let us find the angle between these vectors:
cosθ = (u • v) / (||u|| ||v||)
cosθ ≈ 44 / (7.2 × 8.2)
cosθ ≈ 44 / 59
cosθ ≈ 0.75
θ ≈ arccos(0.75)
θ ≈ 41.4º
For any vector u = <a, b>, the magnitude is given by:
||u|| = √(a2 + b2)
For any two vectors u = <a, b> and v = <c, d>, the dot product is given by:
u • v = ac + bd
The angle between any two vectors u and v is given by:
cosθ = (u • v) / (||u|| ||v||)
Now, let us try an example of each. For these examples let
u = <6, 4>
and
v = <2, 8>.
First, let us find the magnitude of each vector:
||u|| = √(62 + 42) = √(36 + 16) = √52 ≈ 7.2
||v|| = √(22 + 82) = √(4 + 64) = √68 ≈ 8.2
Next, let us find the dot product of these vectors:
u • v = (6)(2) + (4)(8) = 12 + 32 = 44
Finally, let us find the angle between these vectors:
cosθ = (u • v) / (||u|| ||v||)
cosθ ≈ 44 / (7.2 × 8.2)
cosθ ≈ 44 / 59
cosθ ≈ 0.75
θ ≈ arccos(0.75)
θ ≈ 41.4º
Review – Verifying Trigonometric Identities
To verify a trigonometric identity, you need to use existing trigonometric identities to gradually modify one side of the equation and eventually make it look exactly the same as the other side.
Some tips for verifying identities are the following:
- Try to express everything in sin's and cos's.
- Only work with one side of the equation.
Here is an example of a verifying problem; I will list out the steps as I solve it:
cos(–θ) / [1+sin(–θ)] = secθ + tanθ
Use the Even and Odd identities to simplify the terms containing –θ:
cosθ / (1 – sinθ) =
Multiply the numerator and denominator with the conjugate of the denominator:
[cosθ × (1 + sinθ)] / [(1 – sinθ) × (1 + sinθ)] =
Distribute:
(cosθ + cosθsinθ) / (1 – sin2θ) =
Use the Pythagorean identity sin2θ + cos2θ = 1 to change the denominator to cos2θ:
(cosθ + cosθsinθ) / cos2θ =
Split this fraction into two fractions:
(cosθ / cos2θ) + (cosθsinθ / cos2θ) =
Cancel out the cos's:
(1 / cosθ) + (sinθ / cosθ) =
Use the Reciprocal identity 1 / cosθ = secθ and the Quotient identity sinθ / cosθ = tanθ to rewrite the fractions:
secθ + tanθ = secθ + tanθ
Since the LHS (left-hand side) is now equal to the RHS (right-hand side), the verification is done!
Use the Even and Odd identities to simplify the terms containing –θ:
cosθ / (1 – sinθ) =
Multiply the numerator and denominator with the conjugate of the denominator:
[cosθ × (1 + sinθ)] / [(1 – sinθ) × (1 + sinθ)] =
Distribute:
(cosθ + cosθsinθ) / (1 – sin2θ) =
Use the Pythagorean identity sin2θ + cos2θ = 1 to change the denominator to cos2θ:
(cosθ + cosθsinθ) / cos2θ =
Split this fraction into two fractions:
(cosθ / cos2θ) + (cosθsinθ / cos2θ) =
Cancel out the cos's:
(1 / cosθ) + (sinθ / cosθ) =
Use the Reciprocal identity 1 / cosθ = secθ and the Quotient identity sinθ / cosθ = tanθ to rewrite the fractions:
secθ + tanθ = secθ + tanθ
Since the LHS (left-hand side) is now equal to the RHS (right-hand side), the verification is done!
Thursday, May 1, 2014
12.2 - Techniques for Evaluating Limits
In the last section, we learned how to solve basic limit problems. However, not all limit problems can be solved this easily. To solve these, we must learn other techniques for evaluating limits.
The easiest method of evaluating a limit is to use the technique of direct substitution. Simply substitute the value which x is approaching into the function after the limit and solve (this is the same example from the previous blog post, so you can visit that for a more detailed walkthrough):
Substitute 2 into the equation to find the answer:
3(2) – 2 = 6 – 2 = 4
Although, sometimes direct substitution will not work because it will result in indeterminate form, or zero over zero. When this happens, you must use either the cancellation technique or the rationalizing technique.
The cancellation technique involves factoring the numerator and denominator, canceling out common factors, and performing direct substitution again. Here is Example 3 from page 878 of our textbook, which demonstrates the cancellation technique:
Use the rationalizing technique when the numerator or denominator involve roots. With this method, you multiply both the numerator and denominator by the conjugate and perform direct substitution again. Here is Example 4 from page 879 of our textbook, which demonstrates the rationalizing technique:
12.1 - Introduction to Limits
Limits are fundamental to calculus, and this week we have started learning about them. To begin, here is the basic definition of a limit from our textbook:
I am going to use an example from our textbook to demonstrate how to find a limit using a table. The problem is asking us to evaluate the following limit:
First, notice that x is approaching 2. Therefore, we will plug in numbers very close to 2 in order to find the value of the limit. We can try numbers such as 1.99, 1.999, 2.01, 2.001, and so on.
3(1.99) – 2 = 3.97
3(1.999) – 2 = 3.997
3(2) – 2 = ?
3(2.01) – 2 = 4.03
3(2.001) – 2 = 4.003
From these calculations, it appears as though f(x) gets closer to 4 as x gets closer to 2. So, we can conclude that the limit is 4.
We could have also solved this specific problem by substituting the x in the equation with 2, the value which x is approaching:
3(2) – 2 = 6 – 2 = 4
Some limits also fail to exist. Here are the conditions under which a limit will not exist:
Finally, here are the properties of limits and operations that can be performed with limits:
All of these pictures can be found in section 12.1 of our textbook.
Limit Calculator
Since we have been doing limits these past few days, I found a great website for help in solving these types of problems. On this site, you can type in the limit problem exactly as it appears, and the site will solve the problem and show you how it reached that result. This is very useful if you are feeling stuck and need to see the problem worked out. Also, you can see a graph of the limit you entered. Below, I have included a screenshot of a limit I tried out on the site.
Click here for the website!
Click here for the website!
Thursday, April 10, 2014
Vector Calculator
I found this great website that helps with doing vector operations. It can compute magnitudes, dot products, cross products, and more for any 2D or 3D vectors. Also, it can show an explanation to how it reached each answer, so you can follow along if you are confused. I hope this helps you with your future homework or studying!
Click here for the link to this site.
Click here for the link to this site.
Vectors in Space
Earlier this week, we learned about vectors in space. A vector is given by:
v = <v1, v2, v3> (component form)
or
v = v1i + v2j + v3k (unit vector form)
Many operations can be performed with vectors, and, to demonstrate, I will perform these operations with the following vectors:
u = <2, 8, 4>
v = <6, 12, 10>
To find the length (also known as magnitude) of the vector:
||u|| = √(u12 + u22 + u32)
||u|| = √(22 + 82 + 42) = √(4 + 64 + 16) = √84 = ~9.165
To find the sum of the two vectors:
u + v = <u1 + v1, u2 + v2, u3 + v3>
u + v = <2 + 6, 8 + 12, 4 + 10> = <8, 20, 14>
To perform a scalar multiplication on the vector:
cu = <cu1, cu2, cu3>
4u = <4(2), 4(8), 4(4)> = <8, 32, 16>
To find the dot product of the vectors:
u • v = u1v1 + u2v2 + u3v3
u • v = 2(6) + 8(12) + 4(10) = 12 + 96 + 40 = 148
For more information on vector operations, you can visit section 11.2 on page 837 of our book.
v = <v1, v2, v3> (component form)
or
v = v1i + v2j + v3k (unit vector form)
Many operations can be performed with vectors, and, to demonstrate, I will perform these operations with the following vectors:
u = <2, 8, 4>
v = <6, 12, 10>
To find the length (also known as magnitude) of the vector:
||u|| = √(u12 + u22 + u32)
||u|| = √(22 + 82 + 42) = √(4 + 64 + 16) = √84 = ~9.165
To find the sum of the two vectors:
u + v = <u1 + v1, u2 + v2, u3 + v3>
u + v = <2 + 6, 8 + 12, 4 + 10> = <8, 20, 14>
To perform a scalar multiplication on the vector:
cu = <cu1, cu2, cu3>
4u = <4(2), 4(8), 4(4)> = <8, 32, 16>
To find the dot product of the vectors:
u • v = u1v1 + u2v2 + u3v3
u • v = 2(6) + 8(12) + 4(10) = 12 + 96 + 40 = 148
For more information on vector operations, you can visit section 11.2 on page 837 of our book.
The Cross Product of Two Vectors
The cross product of two vectors is a vector that is perpendicular to both. The easiest way to find it is to use matrices, but you can also use this formula:
To find the cross product by using a matrix, create a 3x3 matrix. The first row should be the variables i, j, and k. The second row should be the values of the first vector, and the third row should be the values of the second vector.
For example, this is what the matrix would look like when finding the cross product of the vectors <1, 2, 1> and <3, 1, 2>:
i j k
1 2 1
3 1 2
Now, find the discriminant of this matrix:
Friday, April 4, 2014
Thursday, March 27, 2014
How Much Would You Weigh On the Moon?
I found this very interesting website called "Your Weight On Other Worlds." All you have to do is enter your current weight and click "Calculate," and the website will tell you how much you would weigh on the Moon, Mars, the Sun, and many more. You weigh more or less on different worlds because of the difference in their gravitational pulls. Since the Moon has a weaker gravitational pull than the Earth does, you would weigh less there than you do here. Similarly, since the Sun has a stronger gravitational pull than the Earth does, you would weigh more there than you do here (Source: http://wonderopolis.org/wonder/how-much-do-you-weigh-on-the-moon/).
Click here to visit this website!
Click here to visit this website!
Shapes on Polar Coordinate Systems
When graphing on a polar graph, you can generate some very interesting shapes. Some of these include limaçons, rose curves, circles, and lemniscates.
Limaçons:
r = a ± b cosθ
r = a ± b sinθ
(0 < a, 0 < b)
Rose curves (if n is odd, there will be n "petals"; if n is even, there will be 2n "petals"):
r = a cos(nθ)
r = a sin(nθ)
(n ≥ 2)
Circles:
r = a cosθ
r = a sinθ
Lemniscates:
r2 = a2 sin(2θ)
r2 = a2 cos(2θ)
Here are some specific pictures (from our book) of these graphs:
Limaçons:
r = a ± b cosθ
r = a ± b sinθ
(0 < a, 0 < b)
Rose curves (if n is odd, there will be n "petals"; if n is even, there will be 2n "petals"):
r = a cos(nθ)
r = a sin(nθ)
(n ≥ 2)
Circles:
r = a cosθ
r = a sinθ
Lemniscates:
r2 = a2 sin(2θ)
r2 = a2 cos(2θ)
Here are some specific pictures (from our book) of these graphs:
Polar Coordinate System
This week, we learned about a new system of graphing. Originally, we used the rectangular graphing system, but now we can use the polar graphing system.
On a rectangular graph, a point is defined by (x, y). To reach this point, you must travel x units to the right and y units up. No point can be defined by two different ordered pairs; for example, the point (1, 6) can only be defined by (1, 6).
On a polar graph, a point is defined by (r, θ). To reach this point, you must travel r units in the direction of θ radians. This means that a point can be defined by multiple different ordered pairs; for example, the point (2, π) can also be defined by (-2, 0). This is because traveling 2 units in the direction π is the same as traveling 2 units backwards from the direction 0 or 2π.
To convert from polar to rectangular coordinates, use the following equations:
x = r cosθ
y = r sinθ
To convert from rectangular to polar coordinates, use the following equations:
tanθ = y / x
r2 = x2 + y2
Next, we will learn about graphing lines on polar graphs!
On a rectangular graph, a point is defined by (x, y). To reach this point, you must travel x units to the right and y units up. No point can be defined by two different ordered pairs; for example, the point (1, 6) can only be defined by (1, 6).
On a polar graph, a point is defined by (r, θ). To reach this point, you must travel r units in the direction of θ radians. This means that a point can be defined by multiple different ordered pairs; for example, the point (2, π) can also be defined by (-2, 0). This is because traveling 2 units in the direction π is the same as traveling 2 units backwards from the direction 0 or 2π.
To convert from polar to rectangular coordinates, use the following equations:
x = r cosθ
y = r sinθ
To convert from rectangular to polar coordinates, use the following equations:
tanθ = y / x
r2 = x2 + y2
Next, we will learn about graphing lines on polar graphs!
Thursday, March 20, 2014
Sierpinski Triangle
The Sierpinski Triangle is a very interesting fractal shape. It is an equilateral triangle that contains an infinite number of progressively smaller equilateral triangles. Since it is a fractal, you can zoom into this shape infinitely and never reach the "end," because every time you get closer, more triangles appear around the already existing ones. Here is a video of a Sierpinski Triangle being zoomed into. Enjoy!
Rotations of Conic Sections
Rotating conic sections, such as ellipses, circles, parabolas, or hyperbolas, is most easily done by rotating the axis on which they lie instead. The angle at which the axis is rotated is represented by theta (θ).
The angle θ can be determined by using the following equation:
cot(2θ) = (A – C) / B
The values of x and y can be determined by the following equations:
x = x'cosθ – y'sinθ
y = x'sinθ + y'cosθ
After substituting the value of θ into these equations, the x and y values are determined, and can be substituted into the original equation. Doing so and simplifying should eliminate the xy term, resulting in an equation that can be used to graph the ellipse, circle, parabola, or hyperbola on the rotated axis.
The rotated axis can be created by drawing a set of x and y axes at the angle θ counterclockwise from the original set of x and y axes.
Normally, this process is very complicated at first, especially at the step where you must simplify. If there is still an xy term after you simplify, this is an easy method of seeing that you have done something wrong. If there is not this xy term, simplifying further should make the equation much smaller and easier to read.
Finally, all you have to do is draw the ellipse, circle, parabola, or hyperbola on the rotated axis just as you would draw it on a regular axis!
The angle θ can be determined by using the following equation:
cot(2θ) = (A – C) / B
The values of x and y can be determined by the following equations:
x = x'cosθ – y'sinθ
y = x'sinθ + y'cosθ
After substituting the value of θ into these equations, the x and y values are determined, and can be substituted into the original equation. Doing so and simplifying should eliminate the xy term, resulting in an equation that can be used to graph the ellipse, circle, parabola, or hyperbola on the rotated axis.
The rotated axis can be created by drawing a set of x and y axes at the angle θ counterclockwise from the original set of x and y axes.
Normally, this process is very complicated at first, especially at the step where you must simplify. If there is still an xy term after you simplify, this is an easy method of seeing that you have done something wrong. If there is not this xy term, simplifying further should make the equation much smaller and easier to read.
Finally, all you have to do is draw the ellipse, circle, parabola, or hyperbola on the rotated axis just as you would draw it on a regular axis!
Hyperbolas
Earlier this week, we learned about hyperbolas. Hyperbolas look like two parabolas facing opposite directions. Here are the equations for the two types of hyperbolas:
The best way to explain hyperbolas would be with an example, so here is the equation of an example we will walk through:
The best way to explain hyperbolas would be with an example, so here is the equation of an example we will walk through:
Already, we know that the equation above represents a vertical hyperbola because the y term precedes the x term.
The center of a hyperbola is given by (h, k), but in the equation above, there is neither an h nor a k, so we will set them to 0, making the center (0, 0).
The vertices of a hyperbola are found by adding and subtracting a from the dominant term in the ordered pair of the center. In this case, the dominant term is the y term, which is 0. This gives us the vertices (0, 5) and (0, -5) because the square root of 25 is 5.
The foci are found by adding and subtracting c from the dominant term in the ordered pair of the center, which is the y term again. The value of c squared is the sum of a squared and b squared. After doing this calculation, we find that c = 13 for this particular equation. This gives us the foci (0, 13) and (0, -13).
Finally, we must find the asymptotes. We will use the formulas m = b/a and m = -b/a, where m is the slope. Doing this gives us the asymptotes y = ±(5/12)x.
Now, we have finished finding the information for this hyperbola and can graph it!
Thursday, March 13, 2014
Calculating Pi Using Pies
In honor of Pi day, which is tomorrow, I found a great video showing a few people trying to calculate pi using actual pies! As we all know, pi is equal to the circumference of a circle divided by its diameter. By counting the number of pies placed on the circumference of a chalk circle and dividing it by the number of pies placed on the diameter of the same circle, the people in the video got a number extremely close to the actual value of pi!
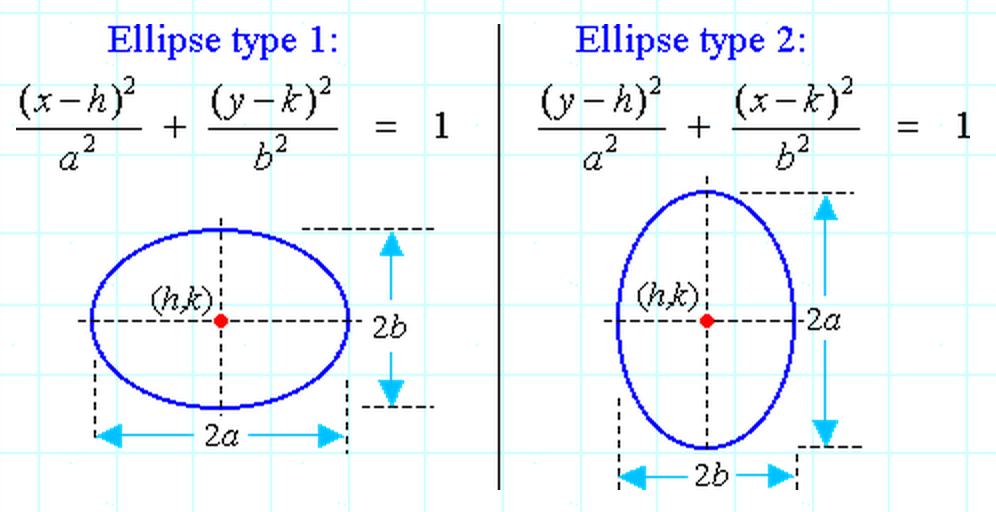
Ellipses
Today, we learned about ellipses. Like parabolas, the two types of ellipses are horizontal and vertical. Here are the equations for these (in this image, Ellipse type 1 refers to a horizontal ellipse while Ellipse type 2 refers to a vertical ellipse):
Two additional values we can determine are c and e.
The value of c is the distance between a focus and the center of the ellipse. It can be calculated using the following equation:
c2 = a2 – b2
The value of e is the eccentricity of the ellipse, or a measure of how oval it is. It can be calculated using the following equation:
e = c / a
On http://www.purplemath.com/modules/ellipse2.htm, I found a great practice problem that I will demonstrate. It asks, "State the center, vertices, foci and eccentricity of the ellipse with the general equation 16x2 + 25y2 = 400."
We should start by putting this equation in the same format as seen in the image above. Since the only difference between the two equations is the switching of a and b, and since we only determine a as being the constant in the denominator greater than that of the other denominator, we can choose either equation. I will choose the first one:
Dividing both sides by 400 and simplifying yields:
(x2 / 25) + (y2 / 16) = 1
Now, we see that the denominator under x is greater than that under y, so we know that a is the square root of the number under x. This gives us:
a = 5
b = 4
We can already determine the center of the ellipse, which is given by (h, k). Looking back at the equation in the image above, we see that h and k are found in the numerators, and because
x2 = (x – h)2 if x = 0
and
The value of c is the distance between a focus and the center of the ellipse. It can be calculated using the following equation:
c2 = a2 – b2
The value of e is the eccentricity of the ellipse, or a measure of how oval it is. It can be calculated using the following equation:
e = c / a
On http://www.purplemath.com/modules/ellipse2.htm, I found a great practice problem that I will demonstrate. It asks, "State the center, vertices, foci and eccentricity of the ellipse with the general equation 16x2 + 25y2 = 400."
We should start by putting this equation in the same format as seen in the image above. Since the only difference between the two equations is the switching of a and b, and since we only determine a as being the constant in the denominator greater than that of the other denominator, we can choose either equation. I will choose the first one:
Dividing both sides by 400 and simplifying yields:
(x2 / 25) + (y2 / 16) = 1
Now, we see that the denominator under x is greater than that under y, so we know that a is the square root of the number under x. This gives us:
a = 5
b = 4
We can already determine the center of the ellipse, which is given by (h, k). Looking back at the equation in the image above, we see that h and k are found in the numerators, and because
x2 = (x – h)2 if x = 0
and
y2 = (y – k)2 if y = 0,
we know that h = 0 and that k = 0, making the center of the ellipse (0, 0).
To determine the vertices, we add and subtract a from the value of the center that is the numerator of a. In this case, this value is 0. This gives us the vertices (5, 0) and (-5, 0).
To determine the foci, we add and subtract c from the value of the center that is the numerator of a.
Again, this value is 0. We determine c using the equation presented earlier, which gives us:
c2 = a2 – b2
c2 = 25 – 16
c2 = 9
c = 3
This gives us the foci (3, 0) and (-3, 0).
Now, all we need to determine is the eccentricity, which is given by c / a:
e = c / a
e = 3 / 5
We have finally finished finding the center, vertices, foci, and eccentricity of this ellipse!
we know that h = 0 and that k = 0, making the center of the ellipse (0, 0).
To determine the vertices, we add and subtract a from the value of the center that is the numerator of a. In this case, this value is 0. This gives us the vertices (5, 0) and (-5, 0).
To determine the foci, we add and subtract c from the value of the center that is the numerator of a.
Again, this value is 0. We determine c using the equation presented earlier, which gives us:
c2 = a2 – b2
c2 = 25 – 16
c2 = 9
c = 3
This gives us the foci (3, 0) and (-3, 0).
Now, all we need to determine is the eccentricity, which is given by c / a:
e = c / a
e = 3 / 5
We have finally finished finding the center, vertices, foci, and eccentricity of this ellipse!
Parabolas
This week, we learned about parabolas. There are two major types of parabolas: vertical and horizontal. Here are the equations for these parabolas:
| Vertical: | (x – h)2 = 4p(y – k) |
| Horizontal: | (y – k)2 = 4p(x – h) |
The vertex of the parabola is given by (h, k), and p is the distance from the vertex to the focus and also the distance from the vertex to the directrix.
Here is an example of a vertical parabola:
Let us assume that h = 2 and k = 4, and focus = (2, 5).
In order to find p, we can use the fact the y-value of the focus is k + p. After substituting in k, we get the following equation:
4 + p = 5
p = 5 – 4
p = 1
That means that the vertex, directrix, focus, and equation would be the following:
Here is an example of a vertical parabola:
Let us assume that h = 2 and k = 4, and focus = (2, 5).
In order to find p, we can use the fact the y-value of the focus is k + p. After substituting in k, we get the following equation:
4 + p = 5
p = 5 – 4
p = 1
That means that the vertex, directrix, focus, and equation would be the following:
| Vertex: | (2, 4) |
| Directrix: | y = k – p = 4 – 1 = 3 |
| Focus: | (2, 5) |
| Equation: | (x – 2)2 = 4(y – 4) |
The next blog post will have information about ellipses!
Thursday, March 6, 2014
The Monty Hall Problem
While we were talking about probability in class, we started talking about the Monty Hall Problem. This probability problem has become famous because it is so counterintuitive. It involves a game show in which the contestant must determine which of three door conceals the grand prize. I do not want to give too much away, so I have included a great video that describes this problem and explains its outcomes. Enjoy!
Mean, Median, Mode, Standard Deviation, and Variance
When working with a set of numbers, measures of central tendency can be used to determine the average, middle, or most occurring numbers. Standard deviation and variance can also be calculated.
Suppose you have the following set of numbers:
4, 2, 7, 4, 3, 1, 8, 5, 6
To calculate the mean, or average, you must divide their sum by the number of numbers:
4 + 2 + 7 + 4 + 3 + 1 + 8 + 5 + 6 = 40
40 / 9 = 4.44
To find the median, you must place all of the numbers in order and find the number in the middle:
1, 2, 3, 4, 4, 5, 6, 7, 8
If there are two numbers in the middle, then the median will be their average; however, the median is only one number in this case.
To find the mode, you must determine which number occurs the most:
1 = 1x
2 = 1x
3 = 1x
4 = 2x
5 = 1x
6 = 1x
7 = 1x
8 = 1x
To find the standard deviation, you must use the following equation:
In this case, the standard deviation is 2.297.
To find the variance, you simply square the standard deviation, producing, in this case, 5.278.
Probability
Today we learned about probability. This is very useful when trying to determine the chance of an event occurring. The probability of an event E occurring is P(E). This can be calculated in different ways depending on the problem itself. Here is an example based on one I saw on http://www.mathsisfun.com/data/probability.html:
A person is rolling two dice and wants to determine the probability of rolling a double, in which the numbers on both dice are the same.
There are only 6 possible outcomes in which the dice are doubles:
{1, 1}, {2, 2}, {3, 3}, {4, 4}, {5, 5}, {6, 6}
The sample space, or set of all possible outcomes contains 36 possible outcomes:
{1, 1}, {1, 2}, {1, 3}, {1, 4}, . . . {6, 3}, {6, 4}, {6, 5}, {6, 6}
Therefore, the chance of rolling doubles is given by:
6 / 36 = 1 / 6 = 0.167 = 16.7%
The probability of any event occurring can only be within the range of 0-1. An event whose probability is 0, or 0%, is called impossible, while an event whose probability is 1, or 100%, is called certain.
An independent event is one whose outcome is not affected by those of other events. An example of this would be flipping a coin; the probability is always 1 / 2 = 0.5 = 50%.
A dependent event is one whose outcome is affected by those of other events. An example of this would be drawing cards from a deck. After the first card is drawn, there is one fewer card in the deck.
A person is rolling two dice and wants to determine the probability of rolling a double, in which the numbers on both dice are the same.
There are only 6 possible outcomes in which the dice are doubles:
{1, 1}, {2, 2}, {3, 3}, {4, 4}, {5, 5}, {6, 6}
The sample space, or set of all possible outcomes contains 36 possible outcomes:
{1, 1}, {1, 2}, {1, 3}, {1, 4}, . . . {6, 3}, {6, 4}, {6, 5}, {6, 6}
Therefore, the chance of rolling doubles is given by:
6 / 36 = 1 / 6 = 0.167 = 16.7%
The probability of any event occurring can only be within the range of 0-1. An event whose probability is 0, or 0%, is called impossible, while an event whose probability is 1, or 100%, is called certain.
An independent event is one whose outcome is not affected by those of other events. An example of this would be flipping a coin; the probability is always 1 / 2 = 0.5 = 50%.
A dependent event is one whose outcome is affected by those of other events. An example of this would be drawing cards from a deck. After the first card is drawn, there is one fewer card in the deck.
Thursday, February 27, 2014
Tau vs. Pi
I recently watched a video explaining the difference between pi and a new constant called tau, which is the equivalent of two times pi. The argument for tau being used is that many equations include two times pi, and that using tau would eliminate this problem and make the equation look simpler. The video itself is somewhat humorous, but it is also very interesting. Enjoy!
Pascal's Triangle
In class this week, we learned about Pascal's Triangle. This is a very useful method of expanding binomials, as I will demonstrate with a quick example.
Imagine that you have the following binomial:
(a + b)^5
To find the coefficients for this expansion, you would have to consult Row 5 of Pascal's triangle:
The coefficients for Row 5 are:
1 5 10 10 5 1
Now, you must place these coefficients before each term. The first term (a) will decrease in power from left to right, while the second term (b) will increase in power from left to right.
(1*a^5*b^0) + (5*a^4*b^1) + (10*a^3*b^2) + (10*a^2*b^3) + (5*a^1*b^4) + (1*a^0*b^5)
When simplified, this is equal to:
a^5 + 5(a^4)(b) + 10(a^3)(b^2) + 10(a^2)(b^3) + 5(a)(b^4) + b^5
Finally, we have expanded this binomial using Pascal's triangle. Expanding the binomial by using the F.O.I.L. method would have also worked, although it would have taken significantly longer and required a much greater amount of work also.
Imagine that you have the following binomial:
(a + b)^5
To find the coefficients for this expansion, you would have to consult Row 5 of Pascal's triangle:
The coefficients for Row 5 are:
1 5 10 10 5 1
Now, you must place these coefficients before each term. The first term (a) will decrease in power from left to right, while the second term (b) will increase in power from left to right.
(1*a^5*b^0) + (5*a^4*b^1) + (10*a^3*b^2) + (10*a^2*b^3) + (5*a^1*b^4) + (1*a^0*b^5)
When simplified, this is equal to:
a^5 + 5(a^4)(b) + 10(a^3)(b^2) + 10(a^2)(b^3) + 5(a)(b^4) + b^5
Finally, we have expanded this binomial using Pascal's triangle. Expanding the binomial by using the F.O.I.L. method would have also worked, although it would have taken significantly longer and required a much greater amount of work also.
Well Ordering Principle
The well ordering principle states that "every non-empty subset of N has a smallest (or first) element" (http://www.proofwiki.org/wiki/Well-Ordering_Principle).
This principle is what we use during mathematical induction. The process for mathematical induction is essentially the following:
Prove that the statement is true for n = 1.
Assume that statement to be true for n + 1.
Prove that the statement is true for n + 1.
By doing this, you will prove that the statement is true for all natural numbers n.
I have found two great videos that explain the process for mathematical induction below. The first one is a bit over 9 minutes long, so I have also included a shorter video if you would not like to spend as much time watching the video.
This principle is what we use during mathematical induction. The process for mathematical induction is essentially the following:
Prove that the statement is true for n = 1.
Assume that statement to be true for n + 1.
Prove that the statement is true for n + 1.
By doing this, you will prove that the statement is true for all natural numbers n.
I have found two great videos that explain the process for mathematical induction below. The first one is a bit over 9 minutes long, so I have also included a shorter video if you would not like to spend as much time watching the video.
Longer video:
Shorter video:
Thursday, February 20, 2014
Why is 0 Factorial Equal to 1?
The factorial of k! is defined as the product of all positive integers from 1 to k. This means that k! can also be written as the following:
k! = k*(k - 1)!
Here is an example:
k = 2
2*(2-1)! = 2
By using this rule, if we set k = 1, then the formula results in the following:
k = 1
1*(1-1)! = 1
1*(0)! = 1
0! = 1
Therefore, 0! is equal to 1.
Finding the n-th Term and Sum of Sequences
Today in class, we learned how to find the nth term of an arithmetic sequence and also how to find the sum of a sequence.
I will start of by explaining the process for finding the nth term of an arithmetic sequence. To provide an example, I will work with the following sequence: 2, 4, 6, 8, ... n. To find the nth term of this sequence, we must use the following equation:
I will start of by explaining the process for finding the nth term of an arithmetic sequence. To provide an example, I will work with the following sequence: 2, 4, 6, 8, ... n. To find the nth term of this sequence, we must use the following equation:
In this equation, a represents the first time of the sequence, and d represents the common difference. The common difference is "the constant added to each element of an arithmetic progression to obtain the next" (definition from: http://en.wiktionary.org/wiki/common_difference).
In this case, a is equal to 2, since 2 is the first term in our sequence. Also, d is equal to 2, because we must add 2 to each term in order to obtain the next term.
Therefore, our equation looks like this:
2 + (n - 1)2
(or, when simplified:)
2n
Now, if we would like to find the 10th term of this sequence, we simply substitute n with 10 in the equation, yielding:
2(10) = 20
Next, I will explain the process of finding the sum of n terms of a sequence (I will use the same sequence as above for this example also).
Taking a closer look at this equation, we can see that this is the same as the following:
(n/2)(a1 + an)
To obtain an, or the nth term, we can simply use the first equation.
Again, let us set n = 10. This means that an = 20.
All we have to do now is substitute these values into the sum equation:
((10)/2)(2 + 20) = 5(22) = 110
Now, we have determined the sum of this arithmetic sequence as well.
Sequences and Sigma Notation
In class on Wednesday, we learned about sequences and summation notation. By using sequences, one can determine the nth term when given a sequence of numbers.
Also, one can determine the sum of a set of numbers by using summation (sigma) notation. Here is a simple example:
The number at the top, 3, is called the upper bound or limit. The number at the bottom, 0, is called the lower bound or limit. In this case, n is the variable that will be used; as you can see, n is set to 0 to begin with.
The process of finding the sum requires you to substitute every value of n (in increments of 1) from the lower limit to the upper limit into the expression to the right of the sigma symbol.
For this example, we would start by substituting 0 (n's starting value) into the expression (2+3n). This yields:
2 + 3(0) = 2
We would repeat this process for every value of n until n was equal to 3:
2 + 3(1) = 5
2 + 3(2) = 8
2 + 3(3) = 11
Now, we take all of the numbers that we have produced and add them together:
2 + 5 + 8 + 11 = 26
Finally, we have determined that the sum of every number from 0-3 when substituted into the expression (2+3n) is equal to 26.
Also, one can determine the sum of a set of numbers by using summation (sigma) notation. Here is a simple example:
The number at the top, 3, is called the upper bound or limit. The number at the bottom, 0, is called the lower bound or limit. In this case, n is the variable that will be used; as you can see, n is set to 0 to begin with.
The process of finding the sum requires you to substitute every value of n (in increments of 1) from the lower limit to the upper limit into the expression to the right of the sigma symbol.
For this example, we would start by substituting 0 (n's starting value) into the expression (2+3n). This yields:
2 + 3(0) = 2
We would repeat this process for every value of n until n was equal to 3:
2 + 3(1) = 5
2 + 3(2) = 8
2 + 3(3) = 11
Now, we take all of the numbers that we have produced and add them together:
2 + 5 + 8 + 11 = 26
Finally, we have determined that the sum of every number from 0-3 when substituted into the expression (2+3n) is equal to 26.
Friday, February 14, 2014
VoiceThread
The following is a link to Group 3's VoiceThread:
https://voicethread.com/?#q.b5433149.i27621334
https://voicethread.com/?#q.b5433149.i27621334
Chapter 8 Review Group 3
Follow this link to visit Group 3's review website!
Friday, February 7, 2014
No Solution or Infinitely Many Solutions in Matrices
When solving a system of equations using matrices, there can be a unique solution, infinitely many solutions, or no solution.
In row-reduced form, the matrix (if it has a unique solution) will consist of a diagonal of 1's surrounded entirely by zeros, and a column of constants to the far right; here is an example:
| 1 0 0 | 4 |
| 0 1 0 | 2 |
| 0 0 1 | 7 |
A matrix with infinitely many solutions has more variables than non-zero rows; here is an example:
| 1 0 3 | 4 |
| 0 1 -2 | 3 |
| 0 0 0 | 0 |
Finally, a matrix with no solution will have a row of zeros on the left side, while the constant on the right side is not 0. A matrix with no solution is called inconsistent; here is an example:
| 1 0 3 | 4 |
| 0 1 -2 | 3 |
| 0 0 0 | 2 |
When graphed, the three types of solutions will look similar to the following image, where consistent and independent means unique solution, consistent and dependent means infinitely many solutions, and inconsistent means no solution.
In row-reduced form, the matrix (if it has a unique solution) will consist of a diagonal of 1's surrounded entirely by zeros, and a column of constants to the far right; here is an example:
| 1 0 0 | 4 |
| 0 1 0 | 2 |
| 0 0 1 | 7 |
A matrix with infinitely many solutions has more variables than non-zero rows; here is an example:
| 1 0 3 | 4 |
| 0 1 -2 | 3 |
| 0 0 0 | 0 |
Finally, a matrix with no solution will have a row of zeros on the left side, while the constant on the right side is not 0. A matrix with no solution is called inconsistent; here is an example:
| 1 0 3 | 4 |
| 0 1 -2 | 3 |
| 0 0 0 | 2 |
When graphed, the three types of solutions will look similar to the following image, where consistent and independent means unique solution, consistent and dependent means infinitely many solutions, and inconsistent means no solution.
Thursday, February 6, 2014
Inverses of Matrices
This week, we learned how to find the inverse of a matrix.
The inverse of a matrix A is written as A-1. When a matrix is multiplied by its inverse, or when the inverse is multiplied by the original matrix, the resultant matrix should have 1's in its main diagonal, while every other entry is 0.
An easy method of finding the inverse of a matrix is to juxtapose a matrix in the desired format to it, and then to perform the basic row operations until the matrix portion on the left looks like the desired matrix. The matrix portion on the right will be the inverse. This might sound a bit confusing, so I will explain the process with a simple 2 x 2 matrix I found on the Internet (by the way, not all matrices are invertible, so some might not have an inverse at all).
The inverse of a matrix A is written as A-1. When a matrix is multiplied by its inverse, or when the inverse is multiplied by the original matrix, the resultant matrix should have 1's in its main diagonal, while every other entry is 0.
An easy method of finding the inverse of a matrix is to juxtapose a matrix in the desired format to it, and then to perform the basic row operations until the matrix portion on the left looks like the desired matrix. The matrix portion on the right will be the inverse. This might sound a bit confusing, so I will explain the process with a simple 2 x 2 matrix I found on the Internet (by the way, not all matrices are invertible, so some might not have an inverse at all).
Here are the steps to solving this matrix:
- Add the first row multiplied by -3 to the second row.
- Divide the second row by -2.
- Add the second row multiplied by -2 to the first row.
Now, we have determined that the matrix on the right side of the vertical line is the inverse of the original matrix.
You can always verify that you have correctly determined the inverse matrix by either multiplying the original matrix by its inverse or vice-versa; if the resultant matrix consists entirely of 0's except for 1's in the main diagonal, then the inverse is correct!
You can always verify that you have correctly determined the inverse matrix by either multiplying the original matrix by its inverse or vice-versa; if the resultant matrix consists entirely of 0's except for 1's in the main diagonal, then the inverse is correct!
Cryptography Worksheet
In class, we went through several aspects of cryptography:
- We found a decryption matrix from an encryption matrix by finding the inverse of the encryption matrix.
- We split the encrypted message into groups of 3, and then multiplied each group of 3 by the decryption matrix in order to find their respective values.
- We used the code 1=A, 2=B, 3=C, and so on, to determine the alphabetical counterpart of each number and to subsequently determine the final message.
- We selected our own invertible matrix and multiplied the resultant number groups from step 2 by this matrix to encrypt the message ourselves.
Here is a picture of this worksheet:
Determinants of Matrices
Today we learned how to find the determinant of any square matrix.
It is fairly easy to find the determinant of a 2 x 2 matrix, where the determinant in the matrix
| w x |
| y z |
is wz - xy.
For a 3 x 3 matrix, several methods of finding the determinant can be used:
Below is an image of the practice problems from today's lesson, which I have completed in UPAD lite:
It is fairly easy to find the determinant of a 2 x 2 matrix, where the determinant in the matrix
| w x |
| y z |
is wz - xy.
For a 3 x 3 matrix, several methods of finding the determinant can be used:
- You can use a shortcut in which the first two columns of the matrix are written to the right side of the last column of the matrix, and then diagonals are formed in order to individually subtract the products of the upward diagonals from those of the downward ones.
- You can use minors and cofactors to solve any square matrix n x n, and this method can be applied to a 3 x 3 matrix, where n = 3.
- If the matrix is triangular, you can find the product of the middle diagonal of the matrix, and this will be the determinant.
Below is an image of the practice problems from today's lesson, which I have completed in UPAD lite:
The following is a link to an Educreations video made in our group:
Thursday, January 30, 2014
Euler's Trail
Solving Matrices Using Gauss Jordan Elimination
Today we learned how to solve systems of equations using augmented matrices and two methods: Gaussian Elimination and Gauss Jordan Elimination.
I will explain the process for Gauss Jordan Elimination below, where the goal is to achieve a leading one in each row of the matrix while every other number in the matrix (except for the rightmost constants) is equal to zero.
To start, here are the problems from Step 1 of our assignment today; in these, I just solved for each variable as usual with systems of equations:
Now, I will demonstrate how to solve such problems using matrices and the Gauss Jordan Elimination method:
First, convert the system of equations into an augmented matrix. Next, perform any of the three elementary matrix operations on the augmented matrix: either switch rows, add rows, or multiply rows. Try to get a leading one in each row while making every other number a zero, except for the constant on the right. Also, it is recommended to work column-to-column from left to right.
Below, I have attached an image of two problems (#1 and #2) from Step 3 from our assignment today, which I have worked out. I also have listed the operation I performed on each matrix to produce it in the right margins.
Link to Prezi
Follow the link below to go to the Prezi presentation!
http://prezi.com/zbgesjwavrrw/?utm_campaign=share&utm_medium=copy
http://prezi.com/zbgesjwavrrw/?utm_campaign=share&utm_medium=copy
Thursday, January 23, 2014
Was Pi Really Going to Be Changed to 3.2?
I just saw a video that I thought was both very strange and also very funny. The video talked about a man named Edward Goodwin who thought he had solved one of the greatest math problems that involved a circle, but there was one problem: for his solution to work, pi had to be 3.2. Even though this is ridiculous and pi is actually ~3.14, he wanted to patent this idea for fear of somebody else using it!
Below, I have included a picture of the problem called "squaring the circle," which is referred to in the video.
Partial Decomposition of Fractions
In this section we covered a variety of topics, and, since I had not created a post for Partial Decomposition of Fractions, I will make that the subject of this post. Below, I have listed the steps for solving such a problem:
1. Identify the factors of the denominator:
5x - 4
x2 - x - 2
5x - 4
(x-2)(x+1)
2. Create a new fraction for each of those factors:
A
(x-2)
+
B
(x+1)
3. Multiply this new set of fractions by the denominator of the first fraction:
A(x+1) + B(x-2)
4. Simplify and combine like terms:
Ax + A + Bx - 2B
5. Factor:
(A+B)x + A - 2B
6. Equate the coefficients to their counterparts in the numerator of the first equation, and solve for their values:
A + B = 5
A - 2B = 4
7. Solve as a system of equations:
A = 14/3
B = 1/3
8. Substitute these values into the equation in Step 2, and that will be the answer:
14
3x-6
+
1
3x+3
1. Identify the factors of the denominator:
5x - 4
x2 - x - 2
5x - 4
(x-2)(x+1)
2. Create a new fraction for each of those factors:
A
(x-2)
+
B
(x+1)
3. Multiply this new set of fractions by the denominator of the first fraction:
A(x+1) + B(x-2)
4. Simplify and combine like terms:
Ax + A + Bx - 2B
5. Factor:
(A+B)x + A - 2B
6. Equate the coefficients to their counterparts in the numerator of the first equation, and solve for their values:
A + B = 5
A - 2B = 4
7. Solve as a system of equations:
A = 14/3
B = 1/3
8. Substitute these values into the equation in Step 2, and that will be the answer:
14
3x-6
+
1
3x+3
Thursday, January 16, 2014
Inflation Calculator
I decided to do my free blog post this week on an inflation calculator I found online. I discovered this calculator when I heard my friend talking about how much he thought a certain item would cost in the early 1900's in terms of today's money. When I looked it up, I found the site very interesting.
For example, if you would like to know how much $5.00 in 1913 would be worth in 2013, you select 1913 in the first option box and 2013 in the second. Once you hit calculate, it will give you the result.
For example, if you would like to know how much $5.00 in 1913 would be worth in 2013, you select 1913 in the first option box and 2013 in the second. Once you hit calculate, it will give you the result.
I was surprised to see that what seemed to be a very small amount of money, $5.00, was worth over $117!
Here is the link to the site if you would like to try it out yourself.
Linear Programming
Linear programming is used to determine the maximum or minimum value of a set of inequalities.
The easiest method of demonstrating this is to provide an example, so I will use #39 on page 581 of our textbook.
It reads: A merchant plans to sell two models of compact disc players at costs of $250 and $400. The $250 model yields a profit of $45, and the $400 model yields a profit of $50. The merchant estimates that the total monthly demand will not exceed 250 units. The merchant does not want to invest more than $70,000 in inventory for these products. Find the number of units of each model that should be stocked in order to maximize profit.
We must first set up the inequalities and determine that x is to represent the $250 model and y is to represent the $400 one. The first inequality will relate the dollar amounts of the items, while the second will relate the number stocked. Also, we must include two "hidden" inequalities, which dictate that there cannot be a negative number of either model of CD players.
250x + 400y ≤ $70,000
x + y ≤ 250
x ≥ 0
y ≥ 0
We should also create an equation to find the maximum profit. We will set z equal to the profit of the $200 model times x plus the profit of the $400 model times y:
z = 45x + 50y
Next we should put the first two inequalities in slope-intercept form (y = mx + b) so that we can graph them (since the last two inequalities are already in an easily graph-able state, we can leave them as-is). This produces:
y ≤ (5/8)x + 175
y ≤ -x + 250
To find the vertices, or the points of intersection, we can use elimination or substitution and solve the inequalities as we would with systems of equations. The x and y values we get as a result will be formatted as an ordered pair (x, y).
We now get the following ordered pairs as vertices:
(0, 0), (250, 0), (0, 175), (200, 50)
All we have to do now is substitute each of these ordered pairs into the equation we created earlier for z and determine which gives the greatest profit:
45(0) + 50(0) = $0
45(250) + 50(0) = $11,250
45(0) + 50(175) = $8,750
45(50) + 50(200) = $11,500
Given that the ordered pair (200, 50) produced the greatest profit, our answer will be:
200 of the $250 CD players
50 of the $400 CD players
The easiest method of demonstrating this is to provide an example, so I will use #39 on page 581 of our textbook.
It reads: A merchant plans to sell two models of compact disc players at costs of $250 and $400. The $250 model yields a profit of $45, and the $400 model yields a profit of $50. The merchant estimates that the total monthly demand will not exceed 250 units. The merchant does not want to invest more than $70,000 in inventory for these products. Find the number of units of each model that should be stocked in order to maximize profit.
We must first set up the inequalities and determine that x is to represent the $250 model and y is to represent the $400 one. The first inequality will relate the dollar amounts of the items, while the second will relate the number stocked. Also, we must include two "hidden" inequalities, which dictate that there cannot be a negative number of either model of CD players.
250x + 400y ≤ $70,000
x + y ≤ 250
x ≥ 0
y ≥ 0
We should also create an equation to find the maximum profit. We will set z equal to the profit of the $200 model times x plus the profit of the $400 model times y:
z = 45x + 50y
Next we should put the first two inequalities in slope-intercept form (y = mx + b) so that we can graph them (since the last two inequalities are already in an easily graph-able state, we can leave them as-is). This produces:
y ≤ (5/8)x + 175
y ≤ -x + 250
To find the vertices, or the points of intersection, we can use elimination or substitution and solve the inequalities as we would with systems of equations. The x and y values we get as a result will be formatted as an ordered pair (x, y).
We now get the following ordered pairs as vertices:
(0, 0), (250, 0), (0, 175), (200, 50)
All we have to do now is substitute each of these ordered pairs into the equation we created earlier for z and determine which gives the greatest profit:
45(0) + 50(0) = $0
45(250) + 50(0) = $11,250
45(0) + 50(175) = $8,750
45(50) + 50(200) = $11,500
Given that the ordered pair (200, 50) produced the greatest profit, our answer will be:
200 of the $250 CD players
50 of the $400 CD players
Solving Systems of Inequalities
We recently learned how to solve systems of inequalities; as opposed to systems of equations, whose solution was the intersection of the lines involved, the solution of a system of inequalities is the graph itself.
Here is a very simple example:
x > 3
y > 5
We can see that x is greater than 3 and y is greater than 5.
To graph this, we can locate the point on the x-axis where x = 3 and draw a vertical line through it. Then we can locate the point on the y-axis where y = 3 and draw a horizontal line through it.
The type of line we need to draw is dependent on the inequality.
- If the inequality has a less than or greater to sign, we need to draw a dashed line because the region does not include the line itself.
- If the inequality has a less than or equal to sign or a greater than or equal to sign, we need to draw a solid line because the region does include the line itself.
Since both of the inequalities contain a greater than sign, both lines will be dashed.
To determine which side of the line to shade, we can substitute any ordered pair into the inequality, and, if the ordered pair satisfies it, we shade that side. If it does not, we shade the opposite side.
The easiest ordered pair to substitute is usually (0, 0), so that is what we will use.
0 > 3 (false)
0 > 5 (false)
Now we see that neither of these inequalities have been satisfied, so we must shade the side that does not include (0, 0).
Points of intersection of the lines are called vertices, and these will be useful in linear programming. Nevertheless, the solution to the system of inequalities is the region which all inequalities in the system include.
Any point within this region is a valid solution to the system.
Therefore, for our example problem, any point whose x position is greater than 3 and whose y position is greater than 5 will be considered a solution.
Any point within this region is a valid solution to the system.
Therefore, for our example problem, any point whose x position is greater than 3 and whose y position is greater than 5 will be considered a solution.
Thursday, January 9, 2014
The "Golden Spiral"
The video talks about a numerical sequence that, when represented as a spiral, can be seen all throughout nature in shells, leaves, and even the formation of galaxies.
The sequence is called the Fibonacci sequence, and looks like this:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34 . . .
You can continue this sequence easily, since the next number is always the sum of the two before it; for example, the 10th number in the sequence is 34 because the two numbers before it, 21 and 13, add up to 34. Therefore, if you wanted to determine the number after 34, you would add 34 and 21 to get 55.
I thought this was very interesting, so I wanted to make it my third blog post for this week.
Solving Systems of Equations That Contain 3 Unknown Variables
The following is a link to the solution of Problem #4 in 7.3 Problems on Edmodo.
http://www.educreations.com/lesson/view/problem-4/15521447/?s=bt50Vf&ref=app
In this example, I will show the steps to solving a system of equations with 3 unknown variables:
4x + y - 3z = 11
2x - 3y +2z = 9
x + y + z = -3
First, we can start by eliminating y from the first two equations. To do this, we need to multiply the top equation by 3.
12x + 3y - 9z = 33
2x - 3y + 2z = 9
After adding these two equations together, we are left with the following:
14x - 7z = 42
Now, we can eliminate y from the two bottom equations. To do this, we need to multiply the bottom equation by 3.
2x - 3y + 2z = 9
3x + 3y + 3z = -9
After adding these two equations together, we are left with the following:
5x + 5z = 0
Next we will eliminate z by using the equation we produces earlier. We will need to multiply the first equation by 5 and the second by 7.
5 * (14x - 7z = 42) = 70x - 35z = 210
7 * (5x + 5z = 0) = 35x + 35z = 0
After adding these two equations together, we are left with the following:
105x = 210
x = 2
Now, we can substitute the value of x, which we have determined is 2, into either of the two equations we produced earlier. I will substitute x into the second one.
5x + 5z = 0
5(2) + 5z = 0
10 + 5z = 0
5z = -10
z = -2
Next, we can substitute the values of x and z into any of the original three equations. I will substitute x and z into the third one.
x + y + z = -3
(2) + y + (-2) = -3
y = -3
Finally, we have determined the values of all 3 variables. Before writing the answer down, we should confirm the answer by substituting these values into one of the first three equations. I will substitute them into the first equation.
4x + y - 3z = 11
4(2) + (-3) - 3(-2) = 11
8 - 3 + 6 = 11
11 = 11
Since the values we found for the variables were valid substitutions for this equation, we can conclude that we have found the correct values. The last step is to present our answer in the following format:
(x, y, z)
Therefore, our final answer is:
(2, -3, 2)
http://www.educreations.com/lesson/view/problem-4/15521447/?s=bt50Vf&ref=app
In this example, I will show the steps to solving a system of equations with 3 unknown variables:
4x + y - 3z = 11
2x - 3y +2z = 9
x + y + z = -3
First, we can start by eliminating y from the first two equations. To do this, we need to multiply the top equation by 3.
12x + 3y - 9z = 33
2x - 3y + 2z = 9
After adding these two equations together, we are left with the following:
14x - 7z = 42
Now, we can eliminate y from the two bottom equations. To do this, we need to multiply the bottom equation by 3.
2x - 3y + 2z = 9
3x + 3y + 3z = -9
After adding these two equations together, we are left with the following:
5x + 5z = 0
Next we will eliminate z by using the equation we produces earlier. We will need to multiply the first equation by 5 and the second by 7.
5 * (14x - 7z = 42) = 70x - 35z = 210
7 * (5x + 5z = 0) = 35x + 35z = 0
After adding these two equations together, we are left with the following:
105x = 210
x = 2
Now, we can substitute the value of x, which we have determined is 2, into either of the two equations we produced earlier. I will substitute x into the second one.
5x + 5z = 0
5(2) + 5z = 0
10 + 5z = 0
5z = -10
z = -2
Next, we can substitute the values of x and z into any of the original three equations. I will substitute x and z into the third one.
x + y + z = -3
(2) + y + (-2) = -3
y = -3
Finally, we have determined the values of all 3 variables. Before writing the answer down, we should confirm the answer by substituting these values into one of the first three equations. I will substitute them into the first equation.
4x + y - 3z = 11
4(2) + (-3) - 3(-2) = 11
8 - 3 + 6 = 11
11 = 11
Since the values we found for the variables were valid substitutions for this equation, we can conclude that we have found the correct values. The last step is to present our answer in the following format:
(x, y, z)
Therefore, our final answer is:
(2, -3, 2)
Wednesday, January 8, 2014
Solving Systems of Equations by Using Substitution
Systems of equations are used to solve a set of equations consisting of two unknown variables. In this post, I will explain how to solve such a set of equations using the substitution method.
Example:
x - y = 0
5x - 3y = 10
First, we need to isolate one of the variables in either of the equations. I will substitute x in the first equation by adding y to both sides.
x = y
Next, we can substitute the value of x in terms of y into the second equation. Since x = y, the second equation can be expressed as the following:
5y - 3y = 10
2y = 10
y = 5
Now that we know the value of y, we can substitute this value into either of our two original equations in order to get the value of x. I will use the first equation.
x - y = 0
x - (5) = 0
x = 5
At this point, we have determined that x = 5 and y = 5. We can substitute these values into either of the two original equations in order to determine if we have gotten the correct result.
x - y = 0
(5) - (5) = 0
0 = 0
Through this process, we have concluded that both x and y are equal to 5.
Also, systems of equations can have three different outcomes:
1. One unique solution: the graphs of the equations intersect at one point.
2. No solution: the graphs of the equations never intersect.
3. Infinitely many solutions: the graphs of the equations are the same.
Subscribe to:
Comments (Atom)

.JPG)


























.JPG)
.JPG)
.jpg)
.jpg)


