Ellipses

Today, we learned about ellipses. Like parabolas, the two types of ellipses are horizontal and vertical. Here are the equations for these (in this image, Ellipse type 1 refers to a horizontal ellipse while Ellipse type 2 refers to a vertical ellipse):

Two additional values we can determine are c and e.
The value of c is the distance between a focus and the center of the ellipse. It can be calculated using the following equation:

c² = a² – b²

The value of e is the eccentricity of the ellipse, or a measure of how oval it is. It can be calculated using the following equation:

e = c / a

On http://www.purplemath.com/modules/ellipse2.htm, I found a great practice problem that I will demonstrate. It asks, "State the center, vertices, foci and eccentricity of the ellipse with the general equation 16x² + 25y² = 400."

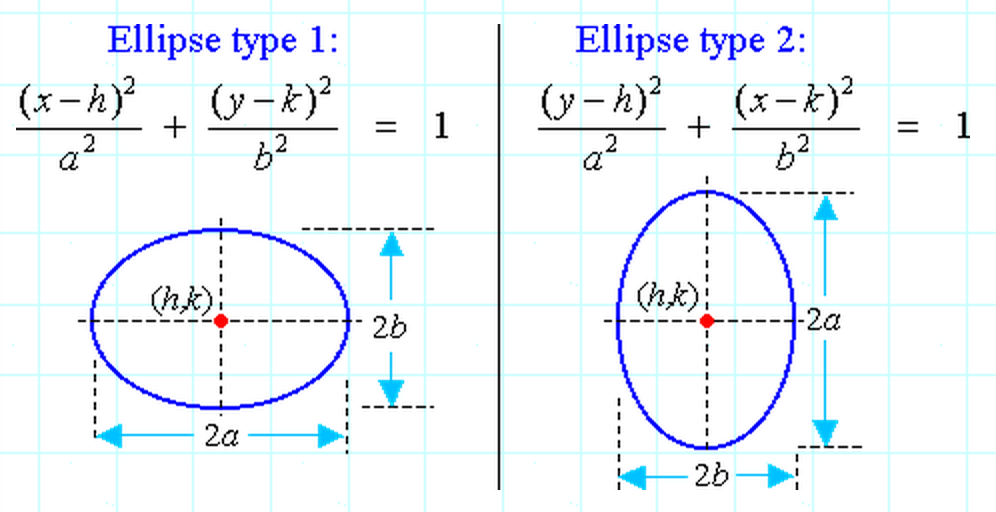
We should start by putting this equation in the same format as seen in the image above. Since the only difference between the two equations is the switching of a and b, and since we only determine a as being the constant in the denominator greater than that of the other denominator, we can choose either equation. I will choose the first one:

Dividing both sides by 400 and simplifying yields:

(x² / 25) + (y² / 16) = 1

Now, we see that the denominator under x is greater than that under y, so we know that a is the square root of the number under x. This gives us:

a = 5
b = 4

We can already determine the center of the ellipse, which is given by (h, k). Looking back at the equation in the image above, we see that h and k are found in the numerators, and because

x² = (x – h)² if x = 0
and

y² = (y – k)² if y = 0,

we know that h = 0 and that k = 0, making the center of the ellipse (0, 0).

To determine the vertices, we add and subtract a from the value of the center that is the numerator of a. In this case, this value is 0. This gives us the vertices (5, 0) and (-5, 0).

To determine the foci, we add and subtract c from the value of the center that is the numerator of a.
Again, this value is 0. We determine c using the equation presented earlier, which gives us:

c² = a² – b²
c² = 25 – 16
c² = 9
c = 3

This gives us the foci (3, 0) and (-3, 0).
Now, all we need to determine is the eccentricity, which is given by c / a:

e = c / a
e = 3 / 5

We have finally finished finding the center, vertices, foci, and eccentricity of this ellipse!